Получение Z-оценки по P-значению
Этот онлайн калькулятор рассчитывает Z-оценку по введенному P-значению
Для стандартного нормального распределения значения Z-оценки для типовых величин P-значения, используемых для проверки гипотез, известны. Например, для значения p=0.05 Z-оценка приблизительно равна 1.64. Однако этот калькулятор вычисляет Z-оценку для любого введенного P-значения. Все что нужно для такого расчета - это иметь возможность рассчитать значение функции, обратной к кумулятивной функции распределения для стандартного нормального распределения. И мы это можем сделать благодаря библиотеке jStat, подключенной к калькулятору. Логика расчета описана под калькулятором.
Ниже приведена логика расчета для разных типов альтернативной гипотезы.
Левосторонняя гипотеза
Для левосторонней гипотезы P-значение это вероятность получить результат равный или меньший чем наблюдаемое значение случайной величины x. В этом случае значение p совпадает со значением кулумятивной функции распределения x, как показано на картинке ниже:
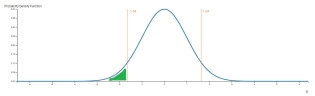
Для того, чтобы найти Z-оценку достаточно найти значение обратной функции к кумулятивной функции распределения.
Правосторонняя гипотеза
Для правосторонней гипотезы P-значение это вероятность получить результат равный или больший чем наблюдаемое значение случайной величины x. В этом случае значение p равно единице минус значение кулумятивной функции распределения x, как показано на картинке ниже:
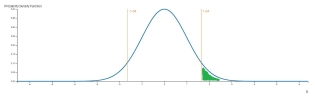
Для того, чтобы найти Z-оценку достаточно вычесть из единицы значение обратной функции к кумулятивной функции распределения.
Двусторонняя гипотеза
Для двусторонней гипотезы P-значение равно удвоенной вероятности меньшего из "хвостов". Так как обычно задают только одно значение p, "хвосты" будут симметричны. В этом случае P-значение равно удвоенному значению кумулятивной функции распределения для левого "хвоста". См. картинку ниже:
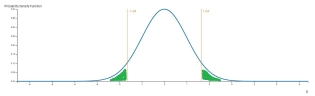
Для того, чтобы найти Z-оценку, достаточно найти значение обратной функции для p делённого на 2. Обратите внимание, что для такого случая калькулятор выдает Z-значение по модулю.
Похожие калькуляторы
- • Биномиальное распределение. Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия
- • Логнормальное распределение
- • Распределение Стьюдента
- • Нормальное распределение
- • Вероятность возникновения некоторого числа событий при проведении нескольких испытаний. Испытания Бернулли.
- • Раздел: Статистика ( 32 калькуляторов )
Комментарии