Объем жидкости в прямоугольном баке под наклоном

Этот калькулятор можно использовать для расчета объема жидкости в прямоугольном баке. Бак может быть наклонен в двух плоскостях (по ширине и длине)
Угол наклона можно задать тремя способами:

• в градусах
• по расстоянию подъема угла бака
• по уровню жидкости в трех разных точках ( точки не должны лежать на одной прямой ).

Внимание расстояние подъема и глубина жидкости должны измеряться перпендикулярно основанию бака, не зависимо от угла его наклона.
Описание методики расчета можно найти сразу за калькулятором.

Объем жидкости в наклоненном прямоугольном баке

Размеры бака

Длина

Ширина

Высота

Наклон

Измерение наклонаУгол Глубина Подъем

Подъем со стороны длины

Подъем со стороны ширины

Угол наклона со стороны длины

Угол в градусах

Угол наклона со стороны ширины

Угол в градусах

Уровень жидкости у самого глубокого угла

Уровень жидкости около угла

Уровень

Тип уровняГлубина жидкости Сухое пространство над поверхностью

Смещение по длине

Смещение по ширине

Уровнь жидкости у соседнего по длине угла

Уровень

Тип уровняГлубина жидкости Сухое пространство над поверхностью

Смещение по длине

Смещение по ширине

Уровнь жидкости у соседнего по ширине угла

Уровень

Тип уровняГлубина жидкости Сухое пространство над поверхностью

Смещение по длине

Смещение по ширине

Точность вычисления

Знаков после запятой: 2

Рассчитать

Объем жидкости

 

Процент заполнения

 

 Ссылка  Сохранить  Виджет

Модель наклонного прямоугольного бака

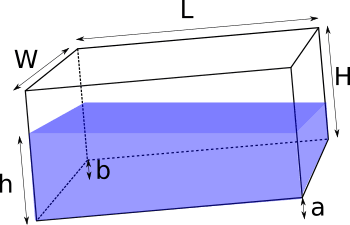
Размеры бака

L - длина
W - ширина
H - глубина

Угол наклона и уровень жидкости

a - расстояние подъема угла, соседнего с самым низким по длине
b - расстояние подъема угла, соседнего с самым низким по ширине
h - уровень жидкости в самом низком углу

Формулы вычисления объема жидкости в наклонном баке

Полагая начало координат совпадающим с нижним углом, ось x откладывается по длине бака L, ось y совпадает с шириной W b ось z - с высотой H выведем уравнение плоскости поверхности жидкости :

Тогда объем жидкости в баке, наклоненном и заполненном так, как на рисунке выше будет равен:

Эта формула справедлива для бака без наклона ( a = b = 0 ) и для наклоненного бака в одной плоскости ( a = 0 или b=0).

Но если начать доливать жидкость и сильнее наклонять бак, то задача становится несколько сложнее.

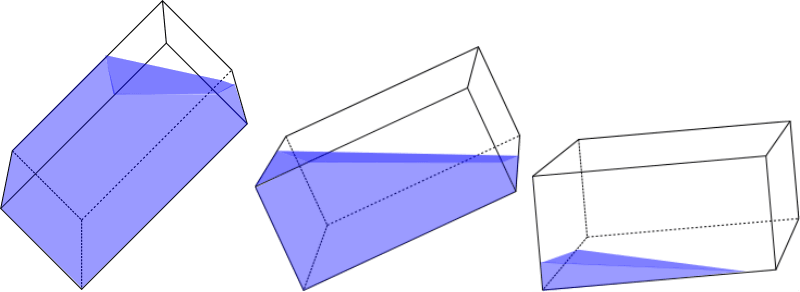
Для бака наклоненного в одной плоскости (b=0) объем будет равен площади заполненного водой сечения умноженное на ширину бака:
,
где

В случае наклона в двух плоскостях (a>0, b>0) вместо выведения формулы для всех возможных комбинаций наклона и уровня жидкости, отметим, что форма жидкости при любом заполнении и наклоне (отличном от нулевого) соответствует усеченной пирамиде.

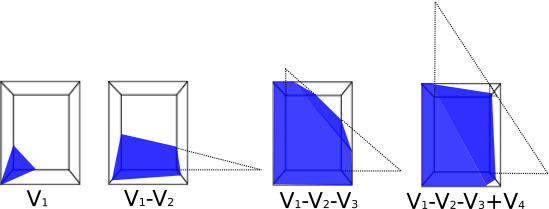
Универсальная формула для вычисления объема выглядит так:

где:
V_i объемы пирамид (иногда усеченных верхней стенкой), образованных тремя перпендикулярными друг другу сторонами бака и плоскостью поверхности жидкости.
V₁ - объем пирамиды вершина которой находится в самом глубоком углу x,y =(0,0)
V₂ - объем пирамиды с вершиной в углу соседнем с глубочайшим углом по длине x,y =(L,0)
V₃ - объем пирамиды с вершиной в углу соседнем с глубочайшим углом по ширине x,y =(0,W)
V₄ - объем пирамиды с вершиной в углу соседнем по диагонали с самым глубоким x,y = (L,W)

Чтобы посчитать каждый из этих объемов V_i нам нужно узнать

• уровень плоскости, совпадающей с поверхностью воды у вершины пирамиды:
  
• сторону нижнего основания по длине (z=0)
  
• сторону верхнего основания по длине z=H
  
• сторону нижнего основания по ширине (z=0)
  
• сторону верхнего основания по ширине z=H
  

Затем можно получить объем по формуле объема пирамиды или усеченной пирамиды:

где