Радиус Земли по широте (WGS 84)
Этот калькулятор определяет радиус Земли на заданной широте, используя референц-эллипсоид WGS 84.
Калькулятор ниже определяет радиус Земли на заданной широте. В реальности, конечно, он рассчитывает радиус референц-эллипсоида WGS 84 на заданной широте, и если вы хотите освежить в голове теорию, вы можете прочитать текст под калькулятором.
Радиус Земли
Поскольку Земля сплющена у полюсов и выпукла у экватора, геодезия моделирует форму Земли сплющенным сфероидом. Сплющенный сфероид, или сплющенный эллипсоид - это эллипсоид вращения, полученный вращением эллипсоида вокруг его короткой оси. Это правильная геометрическая форма, которая почти точно отражает форму Земли. Сфероид, описывающий форму Земли или другого небесного тела называется референц-эллипсоидом. Референц-эллипсоид Земли обычно называют Земной эллипсоид.
Конечно, поверхность Земли имеет неправильную форму. И более точным, чем референц-эллипсоид, приближением этой формы является геоид. Геоид являлся и является важной концепцией геодезии и геофизики уже более двух сотен лет, но работать с ним гораздо труднее, чем с референц-эллипсоидом, так как он тоже имеет неправильную поверхность, зависящую от распределения земных масс.
Собственно, из-за относительной простоты, референц-эллипсоиды и используются для расчета геодезических сетей и определения координат точек в виде широты, долготы и высоты над уровнем моря. В настоящее время наиболее часто используемым референц-эллипсоидом, использующемся также в глобальной системе позиционирования (Global Positioning System - GPS), является референц-эллипсоид WGS 84.
Эллипсоид вращения можно описать всего двумя параметрами. В геодезии используется несколько параметров, но все они эквивалентны или выводятся друг из друга:
- Экваториальный радиус a (или большая полуось), и полярный радиус b (или малая полуось);
- a и первый эксцентриситет e;
- a и геометрическое (полярное) сжатие f.
WGS 84 определяет следующие параметры эллипсоида:
Большая полуось a = 6378137.0 метров
Малая полуось b = 6356752.3142 метра
Точка на поверхности эллипсоида может быть задана параметрическим уравнением кривой
Радиус эллипсоида в данной точке можно найти через теорему Пифагора
Тут есть небольшая проблема, которая заключается в том, что угол t из формулы выше является геоцентрической широтой, а координаты точки, и в частности широта, являются геодезическими, зависящими от используемой системы координат (WGS 84), are geodetic. Геодезическая широта определяется углом между плоскостью экватора и нормалью к поверхности эллипсоида, и геоцентрическая широта - углом между плоскостью экватора и линии, соединяющей точку на поверхности эллипсоида с центром эллипсоида (см. картинку).
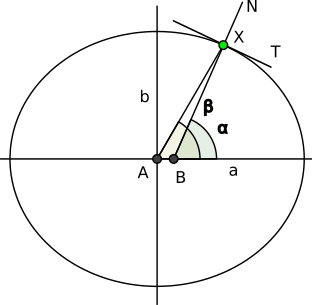
Таким образом, чтобы найти радиус по координатам точки, нам надо от геодезической широты перейти к геоцентрической широте
.
Для начала найдем тангенс касательной к нашей кривой, получив его дифференцируя уравнение кривой.
Это касательный вектор к нашей кривой, идущий вдоль линии T на рисунке.
Мы можем повернуть его на 90 градусов и получить нормаль
, которая указывает вдоль линии N.
Параметр t в выражении выше - это наша . Наклон нормали - это тангенс угла
. Таким образом
или
Используя соотношение между тангенсом и косинусом
и между тангенсом и синусом
,
мы можем переписать формулу для радиуса как
и заменить тангенс тангенсом
Затем, немного упростив, мы получим следующую формулу
И, наконец, формулу, приведенную в википедии
Калькулятор выше как раз и использует эту формулу.
Комментарии