Развертка (выкройка) конуса

Калькулятор рассчитывает параметры развертки прямого кругового конуса на плоскости. Картинка ниже иллюстрирует задачу.

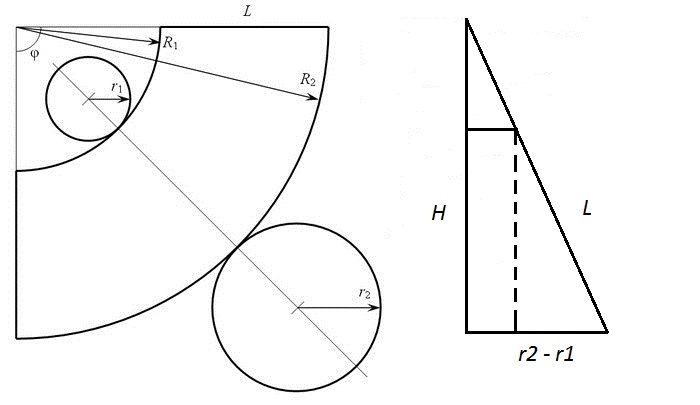
Про конус нам известен радиус основания и высота конуса (или высота усеченного конуса). Для описания развертки нам надо найти радиус внешней дуги, радиус внутренней дуги (если конус усеченный), длину образующей и центральный угол.

Длину образующей можно посчитать по теореме Пифагора:
,
при этом для полного конуса r1 просто обращается в ноль.

Радиус внутренней дуги можно найти из подобия треугольников:
,
опять же, для полного конуса она равна нулю.

Соответственно, радиус внешней дуги:
,
для полного конуса он совпадает с L.

Ну и центральный угол:

Развертка (выкройка) конуса

Радиус основания конуса r2

Высота конуса H

Радиус второго основания r1

Радиус второго основания (для случая усеченного конуса)

Точность вычисления

Знаков после запятой: 2

Рассчитать

Длина образующей L

 

Радиус внешней дуги выкройки R2

 

Радиус внутренней дуги выкройки R1

 

Центральный угол выкройки (в градусах)

 

Длина внешней дуги

 

Длина внутренней дуги

 

Длина хорды, соединяющей края внешней дуги

 

 Ссылка  Сохранить  Виджет