Метод хорд

Немного теории о методе хорд под калькулятором.

Метод хорд

Уравнение

Начальное приближение x0

Начальное приближение x1

Критерий останова (погрешность)

Критерий останова (тип)

Приращение x

Отличие функции от нуля

Точность вычисления

Знаков после запятой: 4

Рассчитать

Формула

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить 

x

 

 Ссылка  Сохранить  Виджет

Метод хорд

Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.

Вывод итерационной формулы аналогичен выводу формулы для метода секущих:

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.

Источник

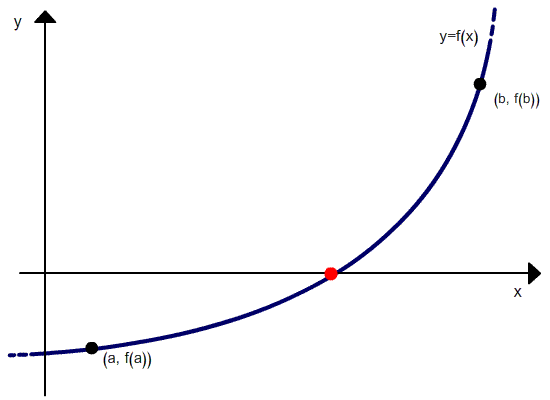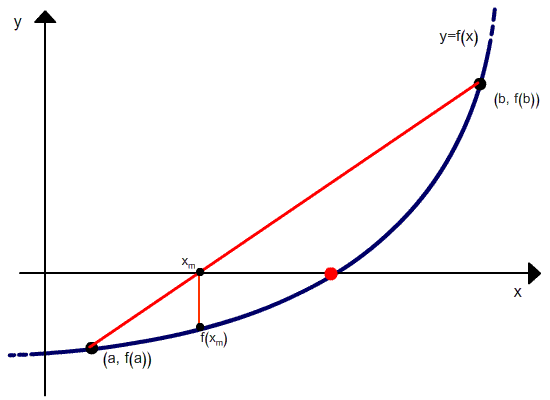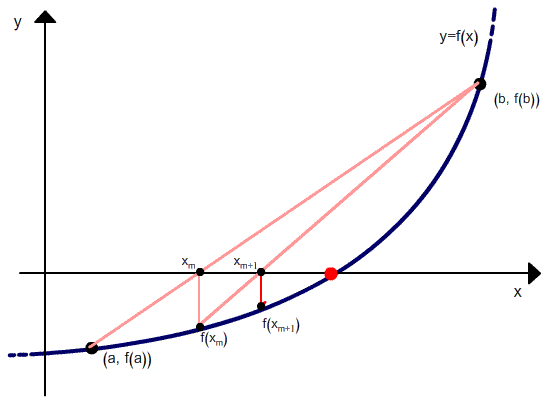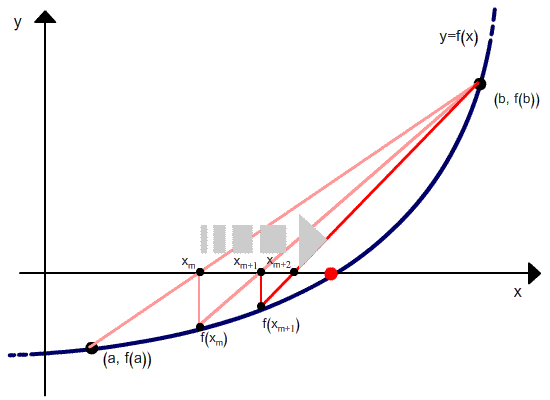
Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.

Подробнее: Метод хорд