Расчет геометрических характеристик плоских сечений простой формы
Этот онлайн калькулятор рассчитывает статические моменты, моменты инерции и радиусы инерции для плоских сечений простой формы
Данный онлайн калькулятор предназначен для вычисления основных геометрических характеристик простейших сечений. Калькулятор выводит пользователю статический момент, момент инерции и радиус инерции по осям x и y, а также координаты центра тяжести и площадь поперечного сечения. Теорию и формулы расчета можно найти под калькулятором.
Левый нижний угол
Правый верхний угол
Центр
Радиус
Вершина при прямом угле
Вторая вершина
Третья вершина
Общий алгоритм расчета следующий:
- Определение центра тяжести поперечного сечения
- Определение площади поперечного сечения
- Определение статического момента
- Определение осевого момента инерции
- Определение радиуса инерции
Статический моменты сечения 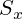 ,
, 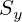 .
.
Физический смысл статического момента: если каждую простую фигуру, из которых состоит сложная фигура, наделить весом, то они будут представлять систему параллельных сил и каждая из них станет создавать свой момент относительно какой-либо оси с плечом, равным расстоянию от оси до центра тяжести данной простой фигуры. Если силу заменить площадью, то момент превратится из силового в геометрический показатель, называемый статическим моментом.1 Измеряется в единицах длины в кубе (см³), может быть положительным, отрицательным и равным нулю.
В общем случае математическая запись статических моментов относительно оси x и y имеет вид:
Для частных случаев, когда рассматриваемая фигура представляет собой простую геометрическую, интегральная запись может быть заменена более простой, тогда формулы выглядят так:
где A - площадь поперечного сечения.
,
- расстояние от осей x и y до центра тяжести простой фигуры.
Центр тяжести прямоугольника расположен в точке пересечения его диагоналей. Центр тяжести окружности совпадает непосредственно с центром самой окружности, а нахождение центра тяжести для треугольника можно найти в этом калькуляторе.
Осевой момент инерции
Осевой момент инерции площади сечения — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Величина осевого момента инерции всегда положительна. Формулы для осевого момента инерции:
Момент инерции фигуры относительно оси, проходящей через ее центр тяжести, называется центральным, или собственным, моментом инерции. Если фигура состоит из нескольких простых фигур, то оси, проведенные через центр тяжести всей фигуры, называются главными центральным осями. Моменты инерции относительно главных центральных осей называются главными центральными моментами.
Приведем формулы главных центральных моментов каждого из используемых в калькуляторе простейших сечений
Прямоугольник
- Площадь поперечного сечения для прямоугольника находится по формуле:
,
где b и h - стороны прямоугольника. - Моменты инерции
и
для прямоугольника находятся по формулам:
Для иллюстрации вывода формул центральных моментов рассмотрим вывод приведенной выше формулы главного центрального момента инерции для прямоугольника.
Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.
Главный центральный момент инерции относительно оси
откуда
Аналогично получим:
Прямоугольный треугольник, катеты которого параллельны осям
- Площадь поперечного сечения для прямоугольного треугольника находится по формуле:
,
где b и h - катеты треугольника. - Моменты инерции
и
для треугольника находятся по формулам:
Круг
- Площадь поперечного сечения для круга находится по формуле:
,
где r - радиус окружности. - Моменты инерции
и
для круга находятся по формулам:
Для нахождения осевого момента инерции относительно произвольной оси воспользуемся теоремой Гюйгенса – Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр тяжести (центрального момента), и произведения площади тела на квадрат расстояния между осями. Измеряется в единицах длины в четвертой степени (см⁴).
Формулы:
Радиус инерции
Радиусом инерции i называют расстояние от соответствующей оси до точки, концентрация всей площади сечения в которой, даст такой же момент инерции, как и для всей площади рассматриваемой фигуры. Измеряется в единицах длины (см).
Формулы:
где A - площадь поперечного сечения,
,
- осевые моменты инерции.
-
Техническая механика для строительных специальностей: учеб. пособие для студ. сред. проф. образования / В.И. Сетков - М.: Издательский центр "Академия", 2007. ↩
Комментарии