Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай - окружности совпадают (это одна и та же окружность) | ||
 |
Окружности не касаются друг друга | |
 |
Одна окружность содержится внутри другой и не касается ее | |

 |
Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше |

 |
Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
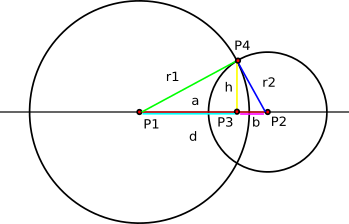
Сначала калькулятор находит отрезок a
и затем отрезок h
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Вторая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Похожие калькуляторы
- • Уравнение окружности, проходящей через три заданные точки
- • Треугольник. Описанная окружность
- • Треугольник. Вписанная окружность
- • Правильный многоугольник. Описанная и вписанная окружность
- • Нахождение центра и радиуса окружности по общему уравнению окружности
- • Раздел: Геометрия ( 99 калькуляторов )
Комментарии