Гидростатическое давление
Калькулятор находит неизвестные величины по заданным, используя формулу давления столба жидкости.
Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости.
Сама формула:
Калькулятор позволяет найти
- давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
- высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
- плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
- ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости
Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения - земное ускорение, и для давления - величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.
Гидростатическое давление — давление столба воды над условным уровнем.
Формула гидростатического давления выводится достаточно просто
Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
В 1648 г. это продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
Также это приводит к такому явлению как гидростатический парадокс.
Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.
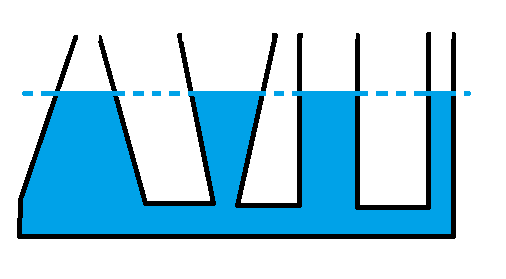
На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда
Источники в википедии: Гидростатическое давление Гидростатический парадокс
Комментарии