PLANETCALC Онлайн калькуляторы

Войти
УчебаМатематикаГеометрия

Эллипсоид

Этот онлайн калькулятор вычисляет объем и площадь поверхности эллипсоида и сфероида.

Неравносторонний эллипсоид

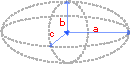
Размеры эллипсоида
Размеры эллипсоида

Эллипсоид - поверхность похожая на сферу, у которой сечение выглядит в виде эллипса.

Эллипсоиды
Эллипсоиды



Выражение стандартного эллипсоида в трехмерной системе координат выглядит следующим образом:
{x^2 \over a^2}+{y^2 \over b^2}+{z^2 \over c^2}=1,
где a - радиус по оси x, b - радиус по оси y, c - радиус по оси z.
Объем эллипсоида задается следующей формулой: {4 \over 3}\pi a b c
Формулу площади поверхности эллипсоида нельзя выразить при помощи простейших фуункций. Кнуд Томсен из Дании предложил следующую приближенную формулу площади поверхности эллипсоида: S\approx 4 \pi [(a^p b^p + a^p c^p + b^p c^p )/3]^{1\over p}, где p=1.6075

PLANETCALC, Эллипсоид

Эллипсоид

Длина (радиус) полуоси a
Длина (радиус) полуоси b
Длина (радиус) полуоси с
Знаков после запятой: 5
Объем
 
Площадь поверхности ( приблизительно)
 

Сфероид

Если две из трех полуосей эллипсоида равны друг другу, то такой эллипсоид называют сфероидом (эллипсоидом вращения). Различают два вида сфероидов: сплющенный сфероид (похожий на линзу) и вытянутый сфероид (по форме напоминающий сигару).
Объем сфероида любого типа вычисляется по формуле: {4 \over 3}\pi a^2 c

В отличие от эллипсоида, для сфероида известна точная формула для вычисления площади поверхности:

Сплющенный эллипсоид вращения (сфероид)
Сплющенный эллипсоид вращения (сфероид)



Для сплющенного сфероида (a = b > c):
S=2\pi\left[a^2+\frac{c^2}{\sin(o\!\varepsilon)} \ln\left(\frac{1+ \sin(o\!\varepsilon)}{\cos(o\!\varepsilon)}\right)\right]
где угловой эксцентриситет o\!\varepsilon=arccos ( {c \over a} )

Вытянутый эллипсоид вращения (сфероид)
Вытянутый эллипсоид вращения (сфероид)



Для вытянутого сфероида (a = b < c):
S=2\pi\left(a^2+\frac{a c o\!\varepsilon}{\sin(o\!\varepsilon)}\right)
где угловой эксцентриситет o\!\varepsilon=arccos ({a \over c} )

PLANETCALC, Сфероид

Сфероид

Знаков после запятой: 5
Объем
 
Площадь поверхности
 
Угловой эксцентриситет (в градусах)
 

Форма Земли похожа на сплющенный сфероид с экваториальным радиусом a ≈ 6,378.137 км и полярным радиусом c ≈ 6,356.752 км. Пользуясь калькулятором можно вычислить площадь поверхности Земли - получается примерно 510 млн. квадратных километров.

Ссылка скопирована в буфер обмена

Похожие калькуляторы

 Геометрия Инженерные объем площадь поверхности сфероид форма Земли эллипсоид
PLANETCALC, Эллипсоид
Anton2020-11-03 14:19:26

Комментарии